几何之利刃——反演变换（1）

现在中考数学越来越爱考反演变换的题目了，于是……就有了这篇文章。

定义

反演变换与平移、旋转、对称变换等类似，也属于一种几何变换，但它更像是作一个图形关于圆的镜像。简单来讲，其定义如下：在同一平面内，有共线的三点 ，其中 为定点，且 ，其中 为常数，则从点 到点 的变换称为“反演变换”，记作 ，那么定点 即反演中心，常数 为反演幂，点 被称为 的反点。对于反演变换 ，令 ，则以反演中心 为圆心， 为半径的圆称为反演变换 的反演圆或基圆，常数 为反演半径。如下图所示。

性质

反演变换的性质有很多条，由于篇幅有限，而且出于入门目的，这里仅简单列举两条易懂且常用的性质。

性质 1：反演变换可逆

由反演变换的定义可知，当 时 的反点时， 也是 的反点，所以点 与 互为反点。

性质 2：（每个点经过反演变换前后的位置关系）

• 位于反演圆上的点，其反点保持在原处。
• 位于反演圆内的点，其反点位于反演圆外。
• 位于反演圆外的点，其反点位于反演圆内。

应用

了解完反演变换的两条基本性质，那么就进入正题：反演变换在初中数学中的应用。

初中数学的反演变换通常会出现在求解动点轨迹的一类问题中，尤其是双动点问题（含一主动点和一从动点），当然部分求最值问题的本质也是求出动点轨迹。

根据反演变换的定义，主动点与从动点的关系必须要满足“定积定角”，需要区分瓜豆原理的“定比定角”。以下会举一个简单的例子进行说明。

平面内有一定点 和两个动点 ，其中点 随点 的运动而运动，现已知点 的运动轨迹，且 ，，其中 为常数， 为定值，请求出点 的运动轨迹。

第Ⅰ类

点 在过点 的直线上运动（线生线）

显然，由于此时 的一边 所在直线固定，则另一边 所在直线也固定，故点 在如图所示蓝色直线（过点 的直线）上运动。动图如下。

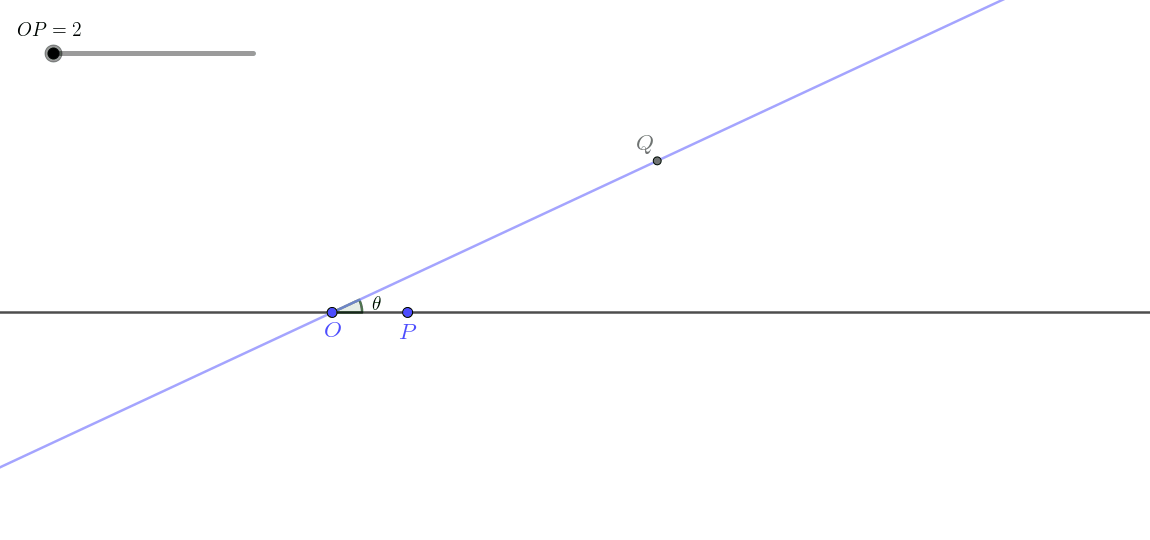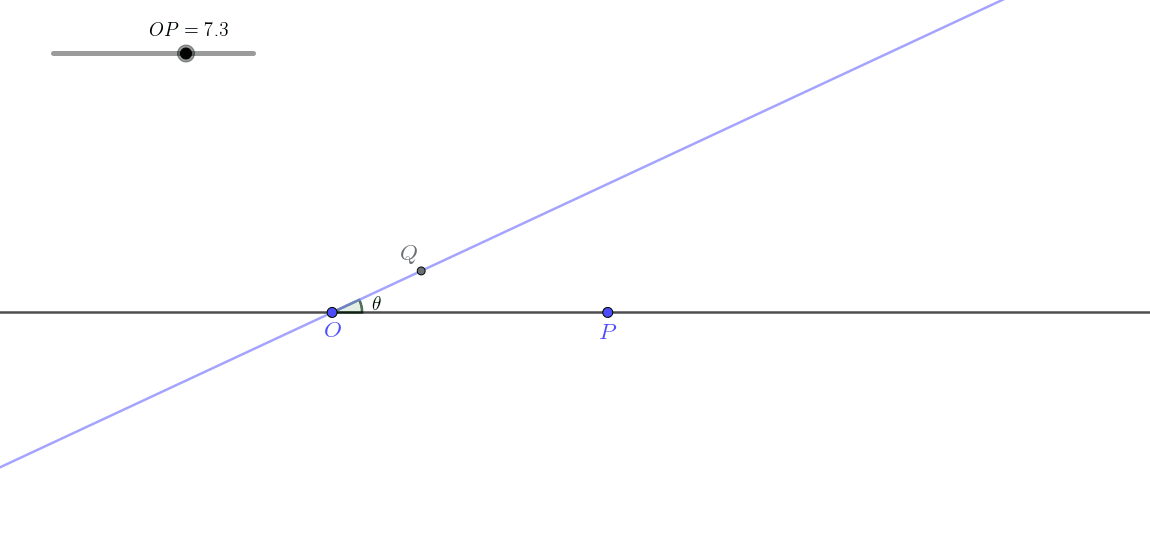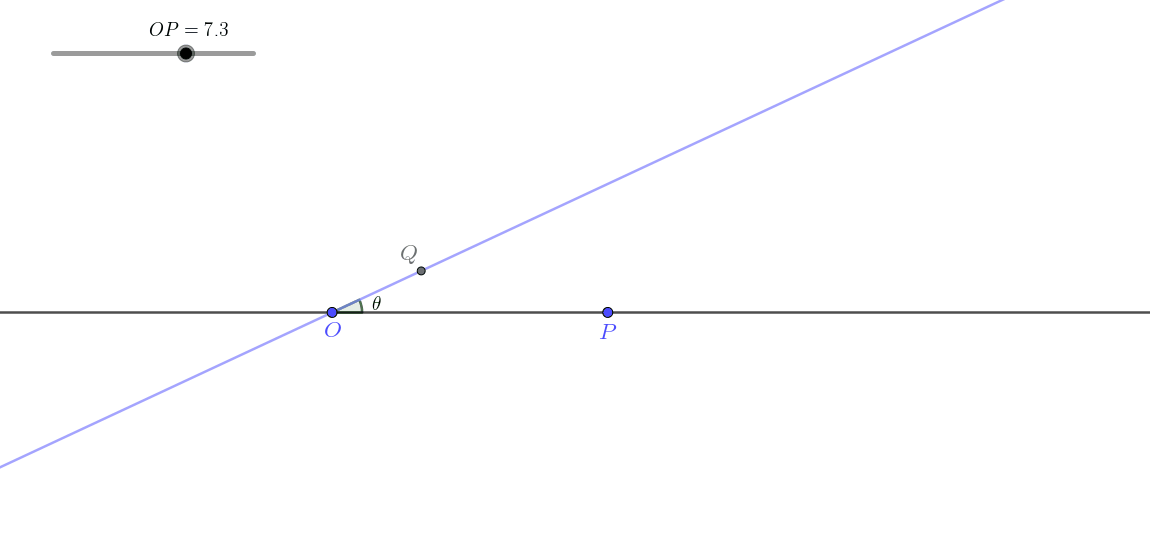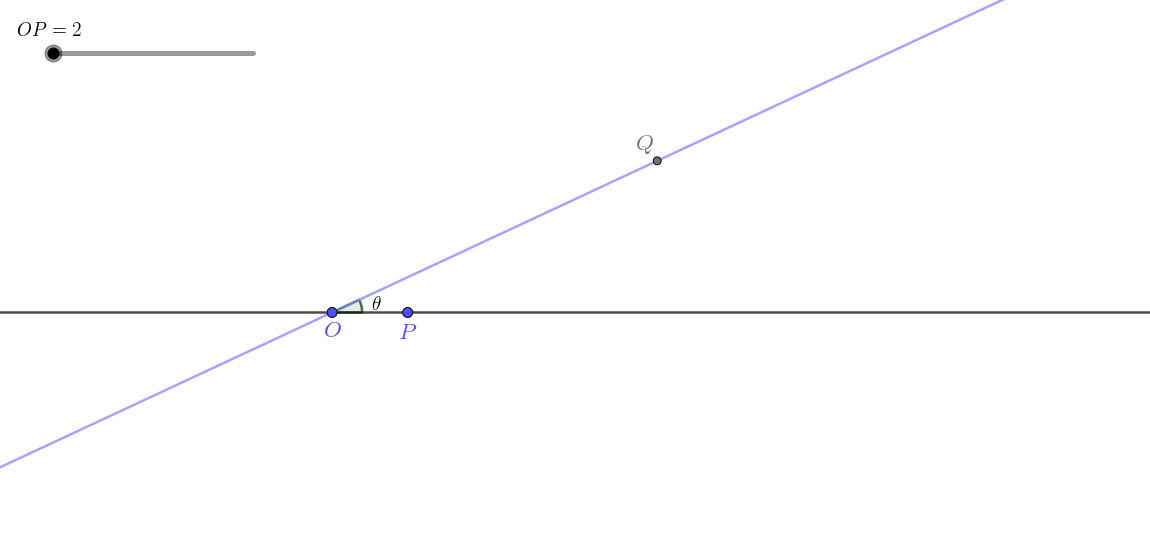
这一类即所谓线生线。

第Ⅱ类

点 在不经过点 的直线上运动（线生圆）

肉眼可见地，这一类与上一类有了天差地别，点 地运动轨迹竟然是个圆！证明如下。 动图如下。

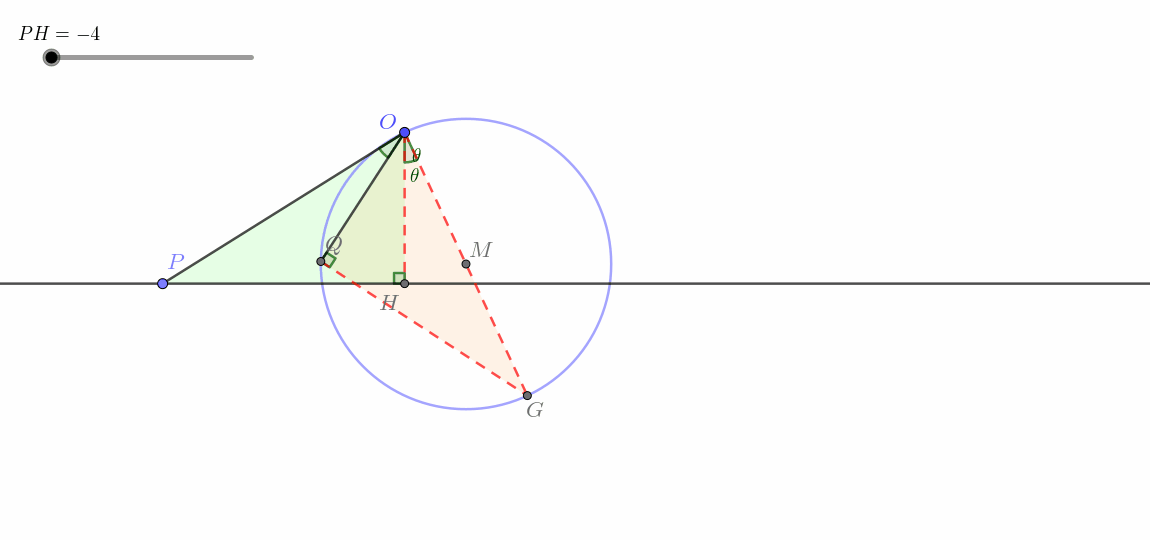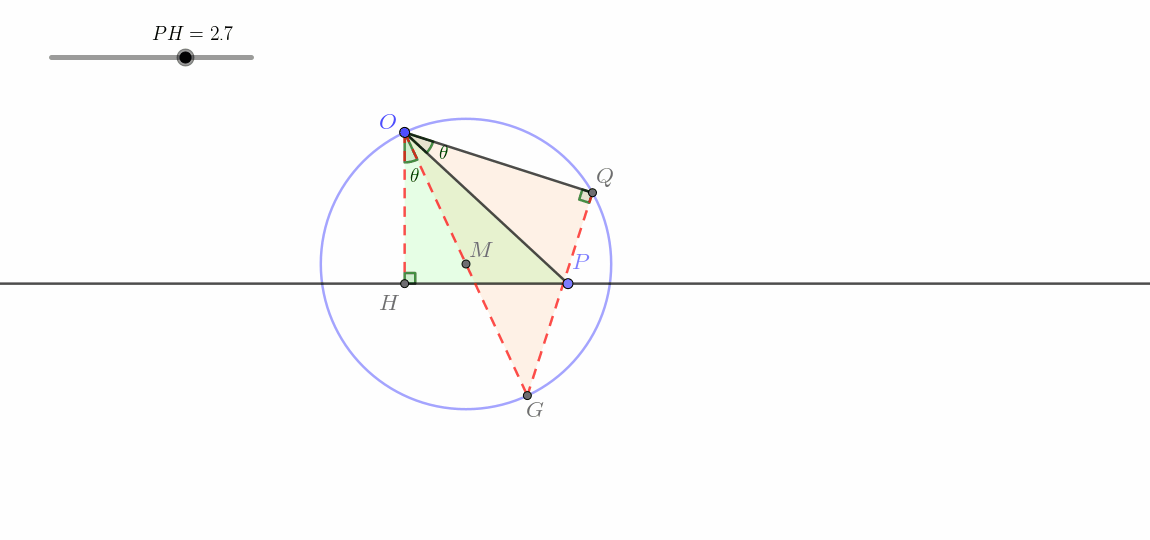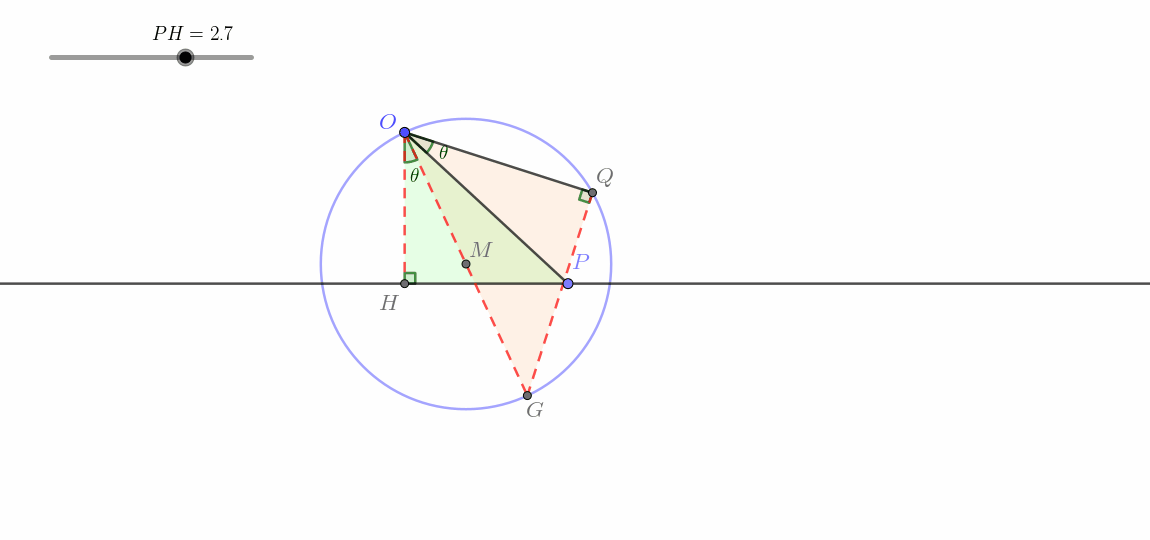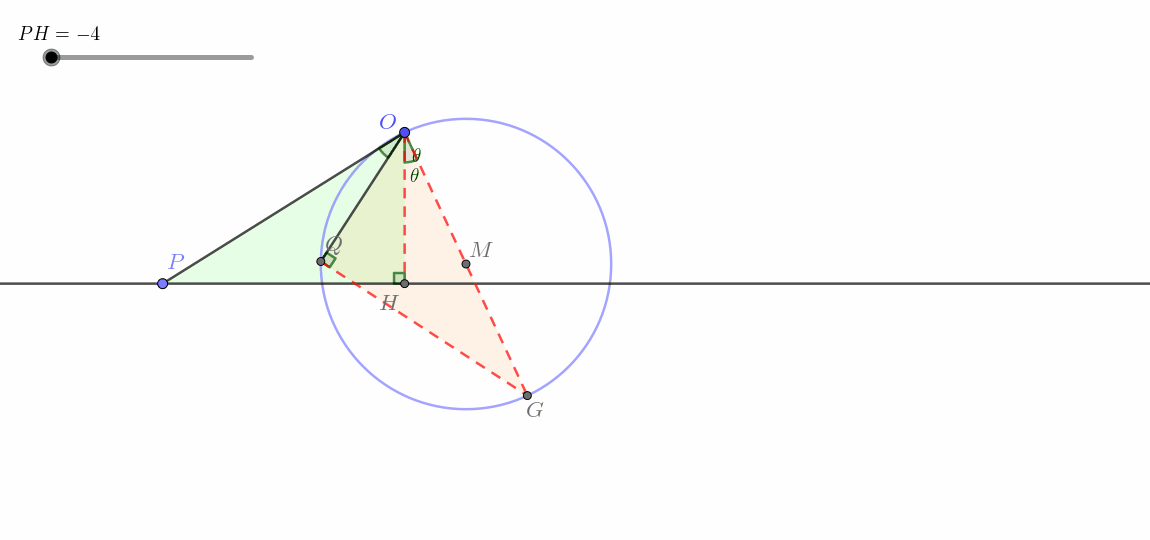
这一类即所谓线生圆。

第Ⅲ类

点 在过点 的圆 上运动（圆生线）

这一类与第Ⅱ类十分类似，只是调换了以下顺序，所以其实时可以直接利用反演变换的性质1（可逆性）来解释。完整证明如下。 动图如下。

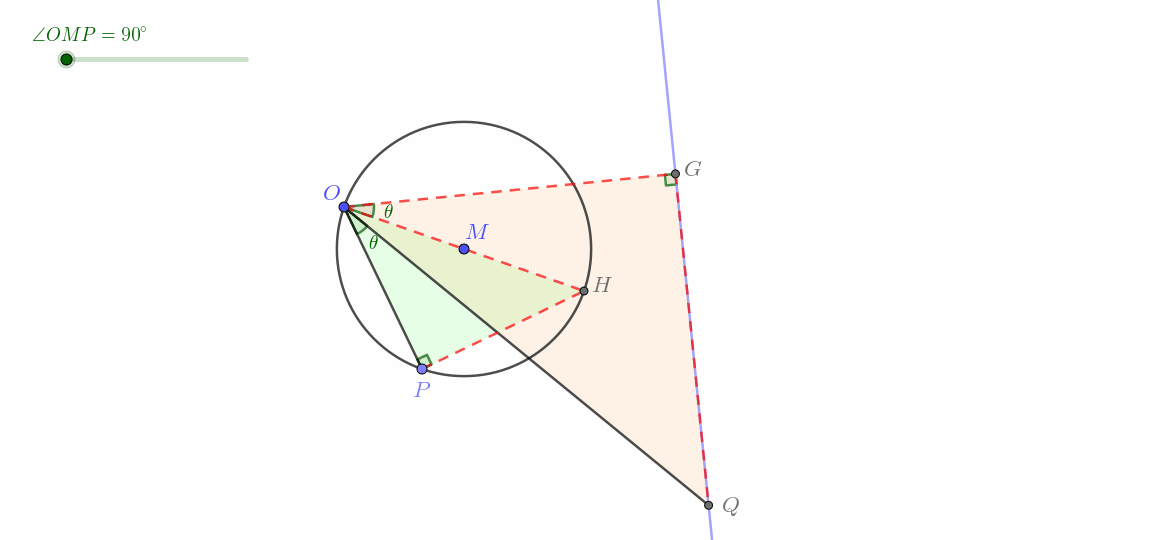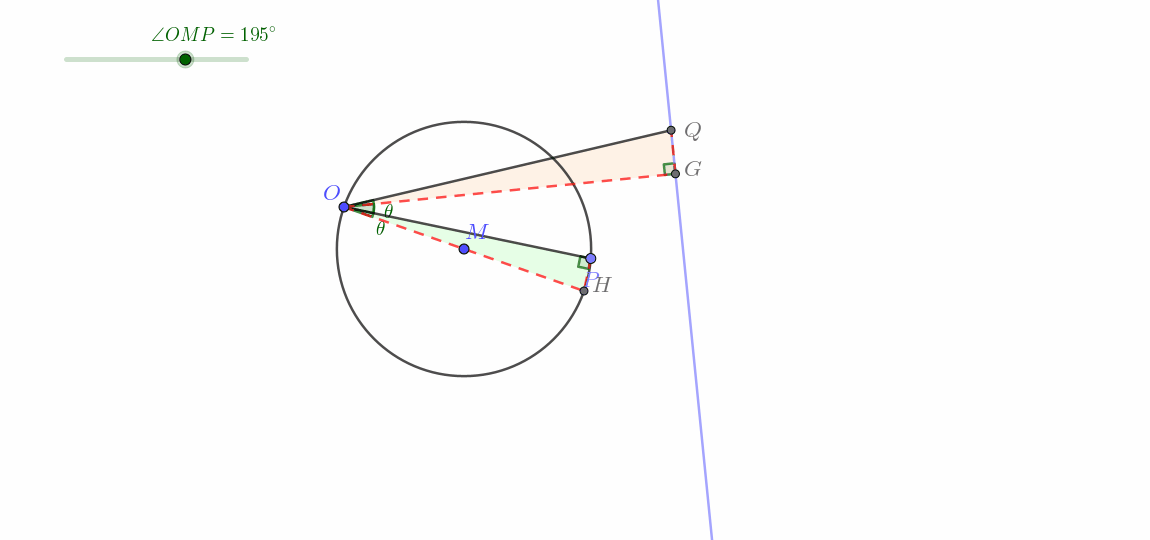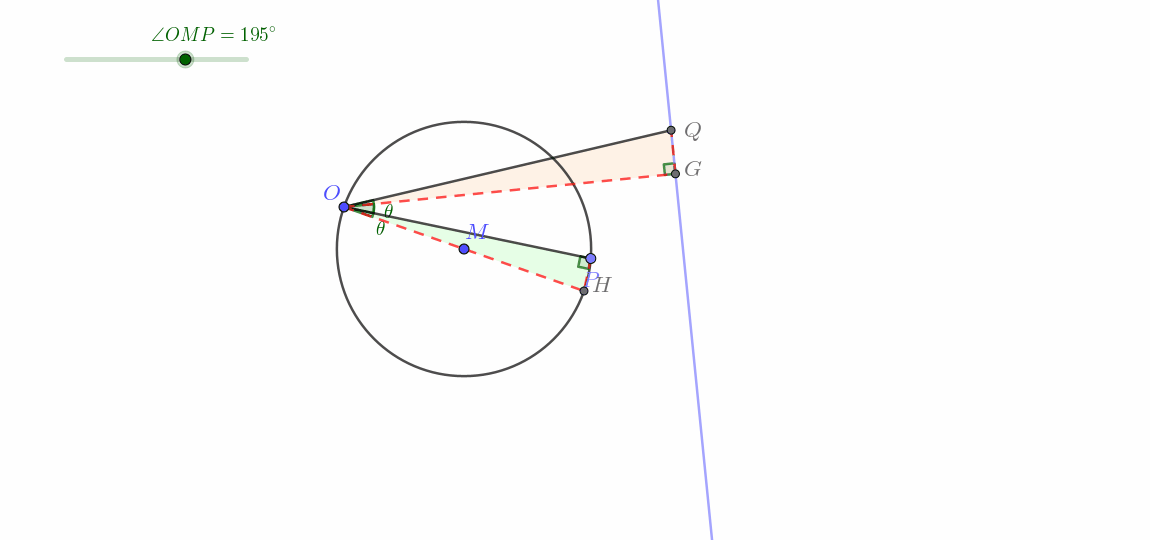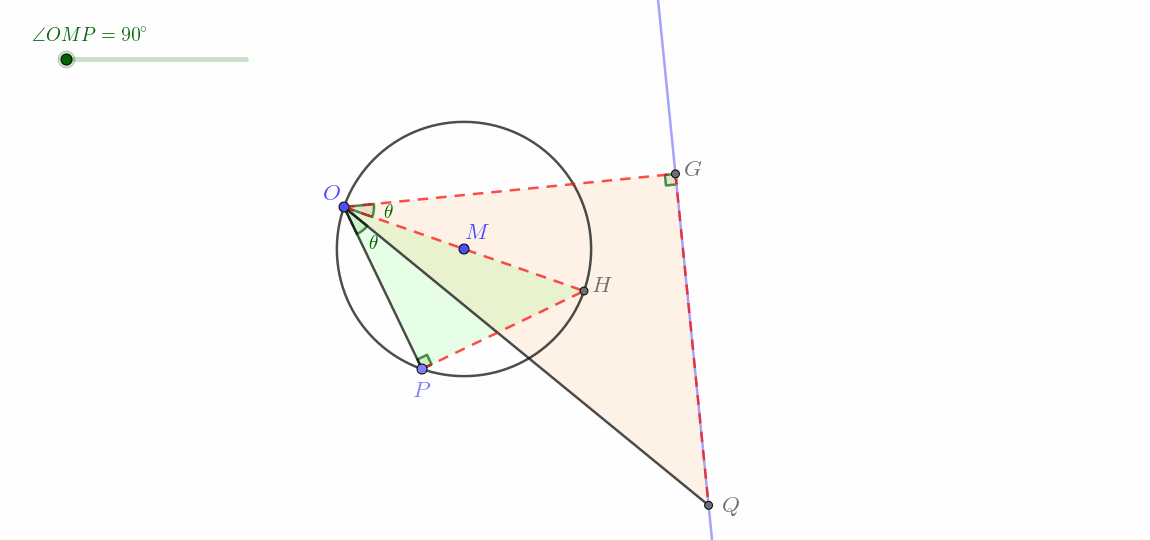
这一类即所谓圆生线。

第Ⅳ类

点 在不经过点 的圆 上运动（圆生圆）

由图可知这一类的做法与前三组更是又显著差异。其实这里用到了“转化”的主要思想，通过将反演问题由圆幂定理进行转化，把题目变为简单的“瓜豆”题。其大致证明如下。 动图如下。

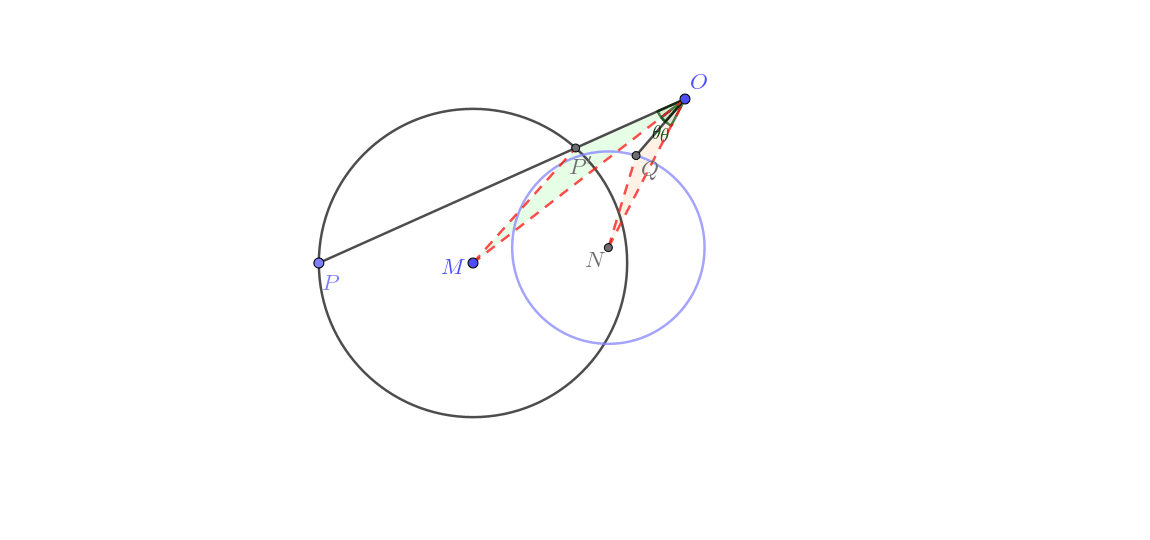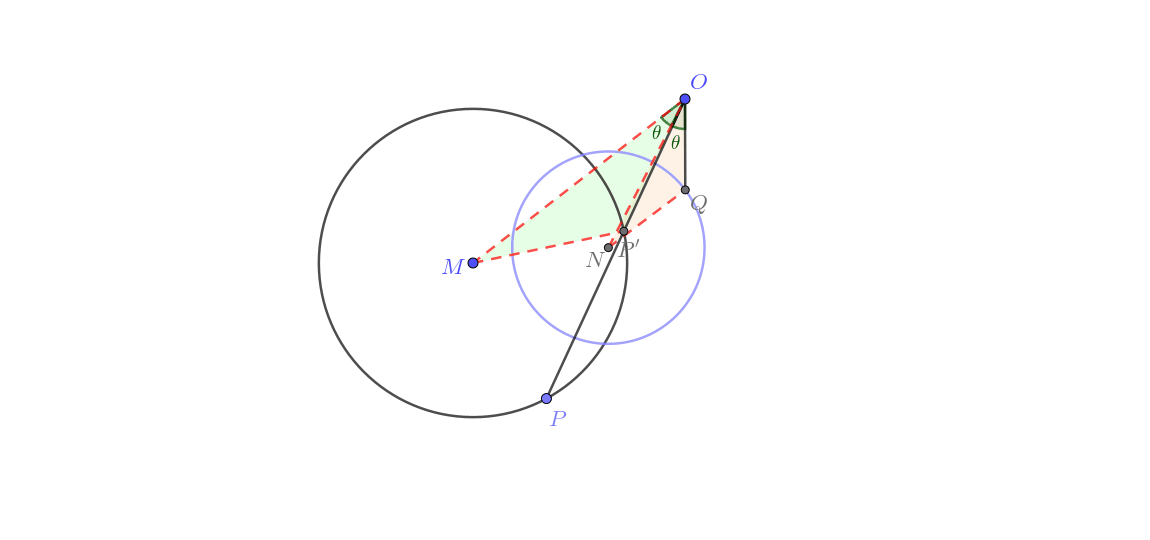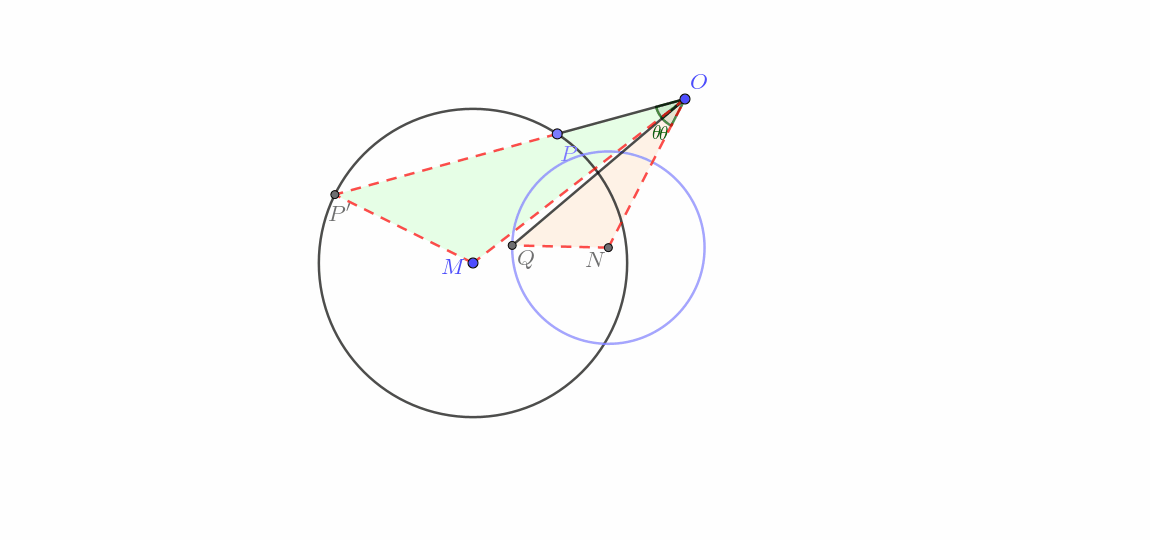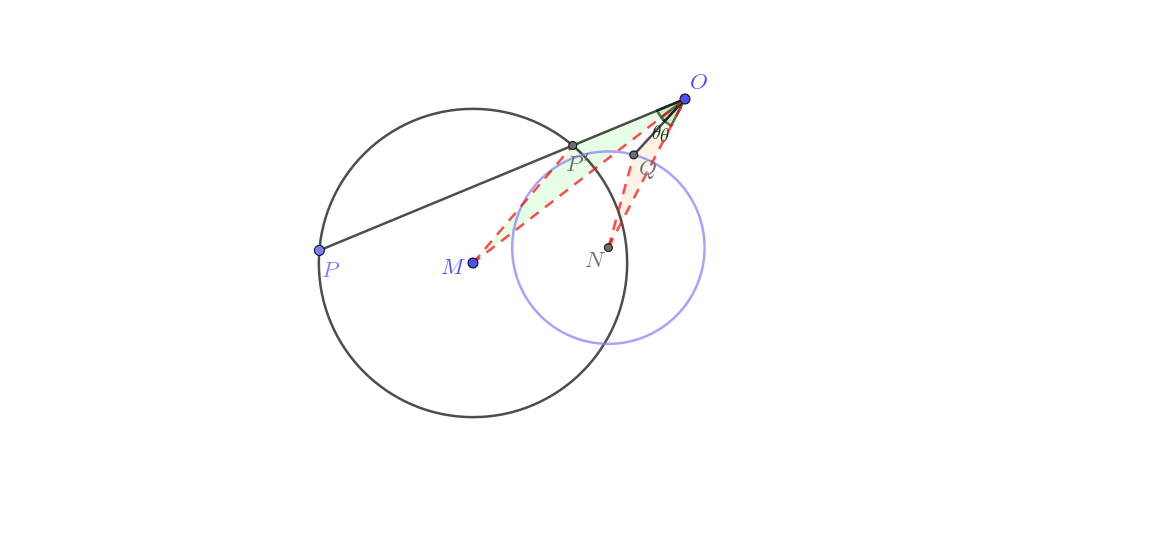
总结

综上所述，反演变换的大多数题目都是由相似解决的，有些甚至还用到了圆幂定理，可见反演变换套路之复杂。当然，以上列举的还仅仅时反演变换最基础的内容，不过即便这样也足以解决 90% 的初中反演类型的题目了，就如2025年广东省广州市越秀区一模卷的第25题第(3)小问，恰好就是反演变换中线生圆的模型题。所以这么重要的知识，还是得好好掌握啊。

读完这篇文章，你也应该差不多已经入门反演变换了，后续我还会出更多相关的内容，希望各位可以动动手指主动分享一下，扩大知识的传播面，让身边更多的人能够了解这些技巧。

EOF (End of File) >_<