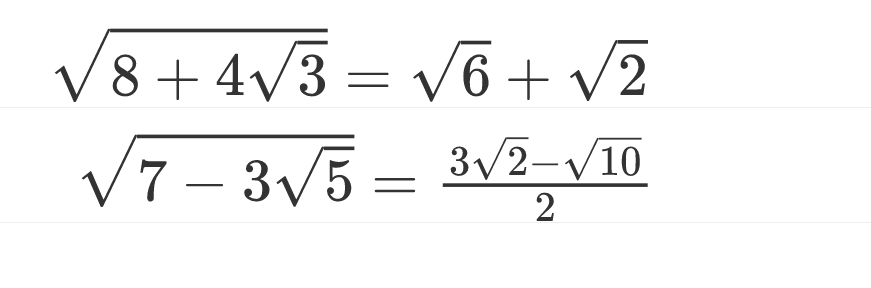关于一道高一上压轴题的深度解析

已经非常非常久没有更新博客了，上一次还是在开学第一周，虽然那一次一次性更了三篇。

所以在今天，迎接2026新年的第二天，我来简单弥补一下吧。

直接进入正题！

这是我校最近一道比较有意思的数学晚测题目，这篇文章将介绍其第(3)问的三种解法，各有优劣，题面如下。

函数图像的绘制

这道题的前两问还是是挺简单的，这里就略过了，主要是我们需要先把 的函数图像画出来，大致如下：

函数图像

函数图像

当然，这个函数图像还是相当好画的，而且也只用画 上的图像。

具体来看，如果去掉绝对值，那这个函数本质上就是平移过后的“对勾函数”，所以最后加上绝对值时只需要把原来“对勾函数”图像的轴下方的部分翻转上来即可。

第(1)(2)问的解答

有函数图像即可知，第(1)问的答案应为 和 。

第(2)问，我们不妨设 ，那么就只需要将四个不等实根分为两组（和 ），对其分别运用韦达定理即可。

第(3)问

我们首先来分析一下这道题的大致解题思路：我们观察题目给定区间 上的函数图像，仅为一段连续的曲线，且在 上单调递增，在 上单调递减，恰好题目又要求 且 上的函数图像单调。由此观之，这题逃不开分类讨论，对此，我们需要在解题时分为两种情况：

其次，需要注意的是，在区间 上，函数 的解析式应写为： 因为 这段区间内的函数图像是从轴下方翻转上来的，所以我们在去绝对值时需要给解析式整体取相反数。

方法一：纯真代数

Ⅰ. 若 ：

我们不难注意到，在区间 上 的函数图像是单调递增的，既然 ，那么必然有 ；同时在区间 上函数 的值域为 ，所以我们可以得到：即： 由ⅰ式，不难得到 既然题目要求的是 的取值范围，那我们不难联想到可以通过 ⅲ式中 的取值范围来确定 的取值范围，这里我们只需要将 当做一个整体，然后 就是关于 的二次函数了，即可利用初中知识简单求解啦。

但是现在的问题就是，我们如何求解 的取值范围呢？

这时候我们再次审视题目条件，并结合此分类依据，可得一条重要的不等式链： 到这一步思路就已经很清晰了，显然，我们需要用 来表示 ，这样我们就可以得到一条只含未知数 的不等式链了，那么求解 的取值范围不就轻而易举了吗？

为此，我们再回到最初的方程组，我们发现这两个方程形式相近，很难不想把它们相加或相减，所以我们进行以下操作：

• ⅰ + ⅱ，得 ，即 ，此时再将等式两边同除以 ，整理得：

• ⅰ - ⅱ，得 ，即 ，此时再将等式两边同除以 ，整理得：

这时候我们通过 ⅳ式和 ⅴ式的等量代换，可以轻松得到 ，整理得： 将这一结果代入刚才的不等式链，得： 解这一不等式链，最终可得： 所以： 此时我们已经求出 的取值范围了！将其代入 ⅲ式的二次函数，可得：

Ⅱ. 若 ：

区别于第 Ⅰ 类，由于 的函数图像在区间 上是单调递减的，所以最初的方程组应为 即： 但这时候，我们很难像第 Ⅰ 类一样迅速用 表示出 了，看起来目标就不太明确了——但是别急！虽然第一步完成不了，但这依旧不妨碍我们先做后面的步骤。

同样地，我们有：

• ⅵ + ⅶ，整理得：

• ⅵ - ⅶ，整理得：

ⅷ + ⅸ，整理得： 天啊😱，我们惊奇地发现 与 的和竟然是个常数！这可是天大的好消息啊，如此一来，我们就可以用 代换 ，也可以用 来代换 了。

那么 ⅵ式就可以转化为： 用 来表示 ，即： 同时我们将 代入上面的不等式链，可得： 解得： 根据二次函数的性质，可得： 代入 ⅹ式，最终可得：

综上所述：

我们已经分类讨论完了两种不同情况，最后将两种情况的结果取并集，得到整道题的最终答案：

方法二：同构方程

Ⅰ. 若 ：

与方法一类似，我们不难得到这样一组方程： 接下来，区别于方法一的点在于，我们不直接用其中一个未知量去表示另一个，而是——构建一个新的一元二次方程！为什么可以这样呢？因为我们发现这个方程组中两个方程的形式完全一样，只有未知量不同，所以我们可以把这两个未知量 和 看作是如下方程的两个不等实根： 将它整理为我们熟悉的一元二次方程，此处同时设该方程一般式等号左边为新函数 ： 这时候这道题就已经转化为一元二次方程中根的分布的问题了，在此题条件下，该一元二次方程要在区间 中有两个不等实根。

到这里，又由于 （因为在区间 上函数 的图像在轴上或其上方即 ，又因为 为正数，所以 ），所以该方程二次项系数为正，那么我们就可以直接列出下列不等式组啦：（其中 为 函数图像即抛物线的对称轴的横坐标） 解该不等式组，可得：

Ⅱ. 若 ：

同样地，我们先列出方程组： 与方法一的第 Ⅱ 类情况相同，我们可以得到： 经过代换，于是： 同构： 整理并设该一元二次方程一般式等号左边为新函数 ： 与第 Ⅰ 类不同的是，我们现在不能马上判断出该方程二次项系数 的正负，所以——这里我们可以尝试利用反证法的思路。

• 假设 ：

  则 ，与题意矛盾，故

• 假设 ：

  因为 ，所以不妨取 ，又因为 ，所以 ；

  而由 原解析式 可知 ；

  两者矛盾，故

综上所述，即 .

至此，我们已较为简便地判断出了该方程二次项系数为负，接下来就同第 Ⅰ 类，可以直接列出下列一元二次方程根的分布不等式组了：（其中 为 函数图像即抛物线的对称轴的横坐标） 解该不等式组，可得：

综上所述：

分类讨论结束后，我们同样对两个结果取并集：

方法三：数形结合

这一种方法的名字一听就很特别吧，那当然——因为这一方法是我博主本人想到的！在班上分享完后还被老师夸了呢！

这一种方法不需要几何脑，也不需要代数脑，几何代数它都只各沾了一点边，所以用这种方法就可以嘲讽出题老师没有水平显得这道题比较简单。

分类讨论之前，我们不妨先在 的函数图像上取两个点 .（均为题中所给的未知量）

Ⅰ. 若 ：

因为在此区间内 单调递增，所以 ，那么就有： 可以得到直线 的解析式为： 不难发现，直线 始终经过原点，为正比例函数，而且其斜率为 。那么接下来就好办了，我们只需要让直线 与 的图像（这一段图像下文简称“曲线”）恰好有两个交点，即符合题意。那我们不妨先把草图画出来：

方法三-第 Ⅰ 类

方法三-第 Ⅰ 类

通过草图，我们可以发现：在直线 与曲线相切时其斜率取到最大值，在经过点 时其斜率取到最小值。

这么看来，我们只需要分别求出直线 在与曲线相切和经过点 时的斜率即可求出 的取值范围。

• 与曲线相切： 转化为一元二次方程，即： 这个方程看起来是不是有点眼熟？没错，它就是方法二第 Ⅰ 类所构造出的方程！但是在这里，我们只需要令其判别式等于零即可求出相切情况的斜率。

  最终解得：

• 经过点 ： 解得：

最后⚠️注意一下边界情况：相切时直线 与曲线有且仅有一个交点，不合题意，所以 不能取到 ；相对地，当直线 经过点 时，它与曲线仍有两个交点，所以 可以取到 .

所以：

Ⅱ. 若 ：

此区间内 单调递减，所以有： 同样可以得到直线 的解析式： 这时候我们发现，这一个解析式只是看上去的话，并没有什么特别的，也不过什么定点之类的。然而，你应该也已经知道了，我们前两种方法都有提到如下等式： 没错，这时候我们的思路仍然同方法一的第 Ⅱ 类情况，即可得到上面 这个恒等式。接下来就简单很多啦，把 代入直线 的解析式并整理，可得： 我们同样惊奇地发现：直线 经过定点 ，而且其斜率为 ，好办了！依照题意，我们同样只需要让直线 和 的函数图像（这段图像下文简称曲线）恰好有两个交点。所以先把草图画出来：

方法三-第 Ⅱ 类

方法三-第 Ⅱ 类

与第 Ⅰ 类类似，我们可以发现：在直线 与曲线相切时其斜率的绝对值取到最大值，在经过点 时其斜率的绝对值取到最小值。

分别如下：

• 与曲线相切： 转化为一元二次方程，即： 这个方程依然与方法二第 Ⅱ 类所构造出的方程相同！同样我们只需令其判别式等于零，解得：

• 经过点 ： 解得：

边界情况：根据草图，可以得知同样为相切时的 不能取，而经过点 时的 可以取到。

所以：

综上所述：

对两类情况的结果取并集，得到最终答案：

后记

这道题的三种解法到这里就分享完了，它们都各有优劣：

• 对于方法一：这一种方法通常适合有计算天赋的同学，其优点是无需过多思考，仅计算；缺点就是对于数学计算功底不佳的同学不友好。
• 对于方法二：该方法适合思维灵活的同学使用，通过观察多条方程式之间的关系与特点来构造新的方程，属于创新了，但其对思维灵活性要求较高。
• 对于方法三：这种方法适合思维比较灵活或擅长几何的同学使用，需要善于发现代数式与图像之间的联系，但通常计算量最小。

总体来说，这一道题目的价值还是非常高的，对同学们的思维训练效果极佳，值得同学们一试！

---

Typora这里显示这篇文章已经四千六百多词了，算是到目前我写过的最长的文章了，但是真的太累了！！！花了我差不多半天时间才写完，结果还要制作封面，生成摘要等等……好苦啊😭😭😭

不过想想这才是2026年的第二天，时间换来质量，我相信这一篇高质量文章一定会给未来带来好运的！💪

您已读完整篇文章~

欢迎随时光顾本站，如您愿意麻烦留步支持一下~